Time Dilation and Relativity

After watching this video lots of questions may popping out from your mind, though I'd also faced the same dilemma "what the crap, how the time can slow down? in my school days I made several time vs "Any dimension" graphs, but in none of them I saw or even dare to took the time in negation. but as time passes and I get involved in my IIT coaching :)  that was the time for one2one with the first torture of my studies viz I.E. Irodov :( 
First time there I got TIME as a dimension (fourth). lots of confusions how to imagine time as a frame of reference and put it into real time physical platform....look similar of trying download  a movie using torrent containing 1GB mirror in a dial up BSNL connection (specially in a  cyber cafe of Kanpur city in the days of year 2k :P)
anyways lets come into the focus:


What is Time Dilation?
One of the most enthralling aspects of Relativity is its new understanding of time.However, time dilation is all but surrealistic.As we all know the speed of light is constant but time cannot be constant. In fact, it doesn't make sense to speak of time as being constant or absolute, when we think of it as one dimension of spacetime. Special Relativity states that time is measured according to the relative velocity of the reference frame it is measured in. Despite of the simplicity of this statement, the relativistic connection between time and space are hard to fathom. There are numerous ways to illustrate this:

The four dimensions of space-time.

In Relativity the world has four dimensions: three space dimensions and one dimension that is not exactly time but related to time. In fact, it is time multiplied by the square root of -1. Say, you move through one space dimension from point A to point B. When you move to another space coordinate, you automatically cause your position on the time coordinate to change, even if you don't notice. This causes time to elapse. Of course, you are always travelling through time, but when you travel through space you travel through time by less than you expect. Consider this example:

Time dilation; the twin paradox.

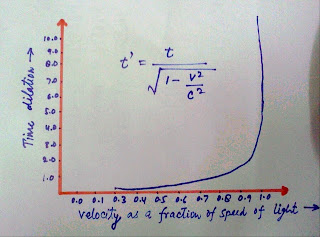
There are two twin brothers. On their thirtieth birthday, one of the brothers goes on a space journey in a superfast rocket that travels at 99% of the speed of light. The space traveller stays on his journey for precisely one year, whereupon he returns to Earth on his 31st birthday. On Earth, however, seven years have elapsed, so his twin brother is 37 years old at the time of his arrival. This is due to the fact that time is stretched by factor 7 at approx. 99% of the speed of light, which means that in the space traveller’s reference frame, one year is equivalent to seven years on earth. Yet, time appears to have passed normally to both brothers, i.e. both still need five minutes to shave each morning in their respective reference frame.

Time in the moving system will be observed by a stationary observer to be running slower by the factor t':

As it can be seen from the above function, the effect of time dilation is negligible for common speeds, such as that of a car or even a jet plane, but it increases dramatically when one gets close to the speed of light. Very close to c, time virtually stands still for the outside observer.

Time expands, space contracts:

Interestingly, while time expands from the perspective of the stationary observer, space contracts from the perspective of the moving observer. This phenomenon is known as Lorentz contraction, which is exactly the reciprocal of the above time dilation formula: l'=l*sqr(1-v²/c²). Thus the space traveller passing by Earth at a speed of 0.99c would see it's shape as an ellipsis with the axis parallel to his flight direction contracted to a seventh of its original diameter. That is of course, if he sees it at all, given the enormous speed. Therefore, space travel is shortened with the velocity of the traveller. A journey to the 4.3 light-years distant Alpha Centauri C, the closest star to our Sun, would take only 7.4 months in a space ship moving at 0.99c.
The effect of time dilation has been experimentally confirmed thanks to very precise caesium clocks that can measure extremely small periods of time. Unfortunately, time dilation is completely outside of human experience, because we have not yet devised a way of travelling at speeds where relativistic effects become noticeable. Even if you spent your whole life in a jet plane that moves at supersonic speed, you would barely win a second over your contemporaries on the ground. And, not even today's astronauts can perceive the Lorentz contraction. Imagine you are a cosmonaut on board of space station Mir, moving at 7700 meters per second relative to Earth. Looking down upon Europe from space, you would see the entire 270 kilometre east to west extent of Switzerland contracted by a mere 0.08 millimetres.
Can we travel at the speed of light?
The hope that one day mankind will be able to travel at near-to-speed-of-light velocities seems farfetched, because of the incredible amounts of energy needed to accelerate a spacecraft to these speeds. The forces are likely to destroy any vehicle before it comes even close to the required speed. In addition, the navigational problems of near-to-speed-of-light travel pose another tremendous difficulty. Therefore, when people say they have to hurry in order to "win time", they probably don’t mean it in a relativistic way.

Life in a space-time cubicle.

From Relativity we learn that time and space is seemingly independent of human experience, as the example of time dilation suggests. Since our own perception of time and space is bound to a single reference frame, time appears to be constant and absolute to us. Physics teaches us that this is an illusion and that our perception deceived us within living memory. Thanks to Einstein, we are now able to draw relativistic spacetime diagrams, compute gravitational fields, and predict trajectories through the four-dimensional spacetime continuum. Still, we are hardly able to visualise this spacetime continuum, or deal with it in practical terms, because human consciousness is bound to the human body, which is in turn bound to a single reference frame. We live within the confinements of our own spacetime cubicle.
Considering that in Relativity, spacetime is independent of human perception, the Kantian understanding of space and time as a priori particulars seems to be obsolete. They are no longer properties of perception, but properties of nature itself. But, there is more trouble looming for Kant. Relativity stretches the distinction between phenomenal reality, i.e. that which can be experienced, and noumenal reality, i.e. that which is purely intelligible and non-sensory, to a degree where these concepts almost appear grotesque. For example, the question arises, whether time dilation falls into the noumenal or phenomenal category? Since it can be measured, it must be phenomenal, however, since human perception is bound to a single reference frame, it must also be noumenal. The distinction between noumenon and phenomenon is thus blurred and possibly invalidated.
We can attempt to imagine relativistic models with the help of appropriate mathematical models, but cannot experience it directly, at least not until someone builds a near-to-speed-of-light spacecraft. I personally thanks to Einstein :) (looks funny), we are able to look beyond the phenomenal reality of space and time, and we understand that there is more to it than commonsense perception tells us. In a way, Einstein has freed our minds from the spacetime cubicle.